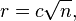• Math & Art: Fermat’s Spiral, Golden Ratio, and Fibonacci Numbers

    Date: 2014.05.06 | Category: Art | Tags:

    FacebookTwitterPinterestTumblrGoogle+
    r = c \sqrt{n},
    \theta = n \times 137.5^{\circ},

    The mathematical equation for a sunflower

    The science part of my brain enjoys fun things like this. Where Fermat’s spiral, golden ratio, Fibonacci numbers combine to make a mind boggling, hypnotic patterns of beauty. However, the technical part of this pattern makes me want to just draw circles at random, not even attempting to replicate it. If you look closely, the lines going toward the middle seem to jumble before they reach the center. To truly see the patter you have to start in the middle, and by the time you reach the edge your basically going around the edge of the circle at a 137.5°angle. Typically, there are 34 spirals in one direction, and 55 in the other. It is actually the most efficient way of packing anything in a circle. Mind boggling. I will have to give it a try for one of my photo realism pieces. Now, to decide what abstract or surrealistic aspect to add to that piece.

    – Krystal Marie